If the earth is spinning at 460 meters per second, or roughly 1,000 miles per hour, and gravity is a weak force, when why don't we fly off the surface of the earth?
There are a number of youtube videos on the internet where people show a tennis ball spinning and water flinging off of it. This is said to represent what would happen the water on the earth if it were spinning. Unfortunately many of the most ridiculous videos have been pulled because the creators have realized that they were in error. Here is one that is still up on youtube.
The reason why they assume the water would fly off is because gravity (over all) is a relatively weak force but a globe spinning at close to 1000 mph is moving very fast.... right?
Sadly, this is just another method of obscuring the truth with large sounding numbers. The spin of the earth is quite slow. Saying that it's spinning 1000 mph is a bit of a misdirection. It only sounds fast. It sounds fast because the metric is difficult to imagine in our everyday lives. Going 1000 mph in a car around a turn is insanely fast. However, 1000 mph on a turn that has a radius of thousands of miles will exert next to no force on an object. Allow me to explain.
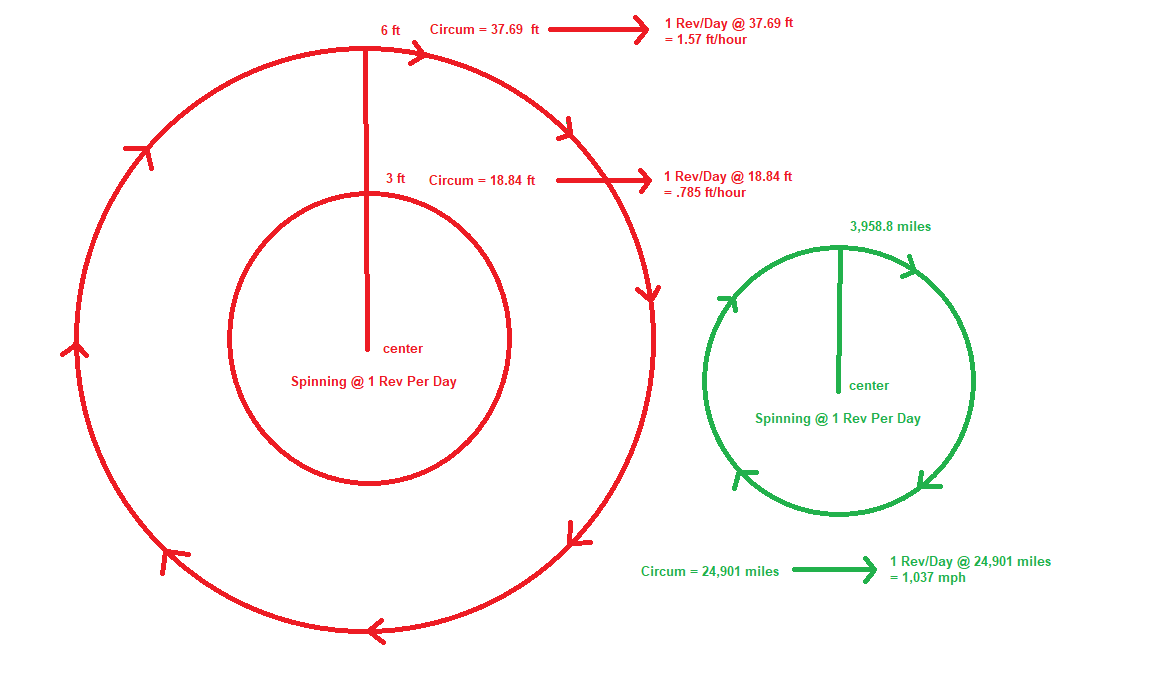
Rotate a tennis ball at the same rotational speed as the earth and see if the water flies off. That is one revolution per 24 hours. That's correct. One revolution for each day. That is how fast the earth spins. I am willing to wager a bet that no water flies off the ball. This is because rotational speed is different than tangential speed.
Rotational speed is a measure of object spinning on an axis. It is the number of revolutions in a given time. Tangential speed is how fast an object on that sphere is moving through space. The larger the sphere, the higher the tangential speed is on the surface, even if the speed of the rotation is unchanged. Tangential speed on a spinning basketball is higher than a tennis ball, even when they are rotating at the same speed.
To demonstrate this principle you can take a yard stick (or anything long like a broom, etc.) and hold it out. Now start slowly spinning. The tip of the object that is furthest from your body will be moving substantially faster than any particular part of your body. If we assume that the tips of the fingers are 3ft from the center of rotation and the end of the yard stick is another 3ft(ish) from the center of rotation, then the tip of the yard stick is now traveling at twice the tangential speed of the finger tips, even though it's rotational speed is identical. The longer the object in your hand is, the higher the tangential speed is, even though it is clear to the observer that both objects are rotating at the same speed.
But there is more to the story. Tangential speed is not equal to a force. Speed and force are correlated but not equal. Thee harder the sphere is that's rotating, the less force is being exerted on the object on the surface. It's the same principle that is at play when we use a long breaker bar to get leverage on a rusty bolt. The further away from the center of rotation, the more force we can exert on the bolt. The inverse is true when calculating centrifugal force being placed on an object that is on/in a rotating system. The further away the from center of rotation, the less centrifugal force is placed on the object.
A prime example of this principle is when we drive a car around a turn. Taking a long country turn at 35 mph is completely different than a turn in the city at 35 mph. The radius of the turn is where the force is generated. This happens because an object in motion wants to stay in motion, in a straight line. This, going around a curve exerts a force on us because our bodies are traveling in one direction but the vehicle is moving is in a slightly different direction. The more divergent that direction is, the more force is placed on us to be in that continuous change on direction.
In conclusion, the earth rotates very slowly. If all the spinning ball demonstrations had the balls spinning at the same actual rate as the earth then they would be embarrassed and would have never posted the video. However, most videos show people spinning balls at a rate 100x or 1000x faster than the earth's rotation. If the earth was spinning 100 times a minute and not once per day, naturally everything on it would overcome gravity and fly off.
If we want to be scientific about it, we can even calculate the amount of force placed on an object based on rotation and mass. The formula for finding centrifugal force (how much for is being applied by the rotation) is F = m * v^2 / r, or Force = mass * velocity^2 / radius.
For my own weight of 175 lbs, the rotational force applied to my body should make me feel roughly .6 pounds lighter than I really am. This is assuming that the radius of the earth is 3958.8 miles, and a tangential speed of 1037 mph.
Summary
The earth does not spin fast enough to fling anything off of it. It only sounds fast because people are not aware of what the 1000 mph is referring to. A much better demonstration can be seen below.
Comments